맨위로가기

깎은 정팔면체

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

깎은 정팔면체는 6개의 정사각형 면과 8개의 정육각형 면으로 이루어진 14면체이다. 부피와 겉넓이는 모서리 길이에 따라 계산되며, 두 종류의 이면각을 갖는다. 깎은 정팔면체는 아르키메데스 다면체 중 하나이며, 면심 입방 격자의 제1 브릴루앙 영역으로 나타나고, 4차 순열 다면체 또는 페르뮤토헤드론으로 묘사될 수 있다. 또한 공간을 채울 수 있으며, 화학에서는 제올라이트 결정 구조에, 고체 물리학에서는 브릴루앙 영역에, 그래프 이론에서는 깎은 정팔면체 그래프로 활용된다. 신라 시대의 주사위인 주령구와 유사한 형태를 가지며, 다양한 분야에서 응용되고 있다.

더 읽어볼만한 페이지

  • 아르키메데스의 다면체 - 다듬은 정육면체
    깎은 정육면체는 정육면체의 꼭짓점을 잘라 만든 다면체로, 6개의 정팔각형과 8개의 정삼각형으로 구성되고, 마름모 입방팔면체 등과 연관되며, 데카르트 좌표계와 트리보나치 수열로 꼭짓점 위치를 나타낼 수 있고, 키랄성 및 팔면체 대칭성을 가지며 여러 분야에 활용됩니다.
  • 아르키메데스의 다면체 - 깎은 정이십면체
    깎은 정이십면체는 정이십면체의 꼭짓점을 잘라낸 아르키메데스의 다면체로, 32개의 면, 90개의 변, 60개의 꼭짓점을 가지며, 축구공, 풀러렌 분자 등 다양한 분야에서 활용된다.
깎은 정팔면체
개요
깎은 정팔면체
깎은 정팔면체
종류아르키메데스 다면체, 평행다면체, 페르뮤토헤드론, 플레시오헤드론, 조노헤드론
면의 수14
모서리의 수36
꼭짓점의 수24
대칭군정팔면체 대칭 (Oh)
쌍대사각육면체
전개도Polyhedron truncated 8 net.svg
꼭짓점 도형Polyhedron truncated 8 vertfig.svg
성질
슐레플리 기호t{3, 4}
위토프 기호2 4 | 3 또는 2 3 3 |
면 구성정사각형: 6, 정육각형: 8
꼭짓점 배열4, 62 (정사각형 1개와 정육각형 2개가 만남)
속성볼록 집합
영어 이름truncated octahedron
기타 정보
부피8√2 a³ (a는 모서리 길이)
겉넓이(6 + 12√3) a² (a는 모서리 길이)

2. 성질

깎은 정팔면체는 정팔면체의 각 꼭짓점을 잘라내어 만든 아르키메데스 다면체 중 하나이다. 6개의 정사각형 면과 8개의 정육각형 면으로 구성되며, 총 14개의 면을 가진다. 쌍대다면체는 사각육면체이다.

깎은 정팔면체의 3D 모델

  • 별 다면체의 수: 42개 (겉면 15개, 뒷면 27개)
  • 외접구 반지름: 한 변의 길이를 a라고 할 때 \frac{\sqrt{10}}{2}a

2. 1. 부피와 겉넓이

한 모서리의 길이가 a인 깎은 정팔면체의 부피 V와 겉넓이 S는 다음과 같다.

  • '''부피''': V = 8\sqrt{2} a^3 \approx 11.3137 a^3
  • '''겉넓이''': S = (12\sqrt{3}+6)a^2 \approx 26.7846 a^2


깎은 정팔면체의 부피는 원래 한 변의 길이가 3a인 정팔면체의 부피에서, 한 변의 길이가 a인 6개의 정사각뿔 부피를 빼서 구한다.

한 변의 길이가 3a인 정팔면체의 부피는, 한 변의 길이가 3a인 두 개의 정사각뿔을 180도 회전시켜 붙인 형태이므로, 정사각뿔 부피의 2배이다. 정사각뿔의 밑면 넓이(S)는 S=(3a)^2=9a^2이고, 높이(h)는 피타고라스 정리를 이용하여 \sqrt{(3a)^2 - (3\sqrt{2} a / 2)^2} = 3\sqrt{2}a / 2로 계산할 수 있다. 따라서 정팔면체의 부피는 V = 1/3 \times S \times h \times 2 = 1/3 \times 9a^2 \times 3\sqrt{2}a/2 \times 2 = 9\sqrt{2}a^3이다.

한 변의 길이가 a인 정사각뿔의 넓이(S)는 S=a^2이고, 높이(h)는 h=\sqrt{(a)^2 - (\sqrt{2}a/2)^2} = \sqrt{2}a/2이다. 따라서 정사각뿔의 부피는 V = 1/3 \times a^2 \times \sqrt{2}a/2 = \sqrt{2} a^3 /6이다.

그러므로 깎은 정팔면체의 부피는 V = 9\sqrt{2} a^3 - 6 \times \sqrt{2} a^3/6 = 8\sqrt{2} a^3 \approx 11.3137 a^3이다.

깎은 정팔면체의 겉넓이는 8개의 육각형과 6개의 정사각형의 넓이를 더한 값이다. 따라서 깎은 정팔면체의 겉넓이는 8(3\sqrt{3} a^2 /2) + 6(a^2) = 12\sqrt{3}a^2 + 6a^2 = (12\sqrt{3}+6)a^2 \approx 26.7846 a^2이다.

2. 2. 이면각

깎은 정팔면체는 두 가지 종류의 이면각을 가진다. 정육각형끼리 만나는 경우의 이면각은 정팔면체에서 정삼각형끼리 만나는 경우와 같으며, 그 값은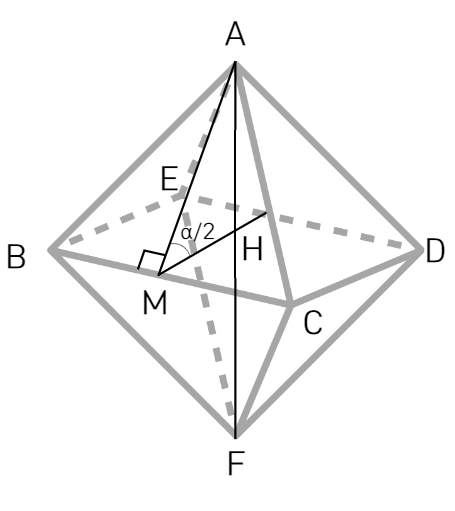 \arccos\left ( -\frac{1}{3} \right )\approx 109.47^\circ이다.

정팔면체 이면각


정육각형과 정사각형이 만나는 경우의 이면각은 정사각뿔에서 밑면과 옆면이 이루는 각을 \alpha라 할 때, \pi-\alpha 와 같으며, 그 값은 \arccos\left ( -\frac{1}{\sqrt{3}} \right ) \approx125.26^\circ이다.

2. 3. 좌표

변의 길이가 1인 깎은 정팔면체의 꼭짓점의 데카르트 좌표는 다음 값들의 모든 순열이다.

:\bigl(\pm\sqrt{2}, \pm\tfrac{\sqrt{2}}{2}, 0\bigr).

2. 4. 대칭

깎은 정팔면체는 정팔면체와 동일한 3차원 대칭군인 정팔면체 대칭 O_h를 갖는다.[3] 각 꼭짓점은 정사각형 하나와 정육각형 두 개로 둘러싸여 있으며, 꼭짓점 도형은 4 \cdot 6^2로 표시된다.[4]

3. 분류

깎은 정팔면체는 13개의 아르키메데스 다면체 중 하나이며, 쌍대다면체는 사각육면체이다.[3] 이 둘은 모두 정팔면체 대칭 \mathrm{O}_\mathrm{h} 를 갖는다.[4] 각 꼭짓점은 정사각형 하나와 육각형 두 개로 둘러싸여 있으며, 꼭짓점 도형은 4 \cdot 6^2 로 표시된다.[5]

깎은 정팔면체는 공간을 채울 수 있는 근접다면체 중 하나로, 대칭적인 들로네 집합의 보로노이 셀로 정의된다.[3] 깎은 정팔면체를 포함하여 5개의 3차원 기본 평행다면체가 존재한다.[4]

또한 깎은 정팔면체는 4차 순열 다면체(4-permutohedron)로 묘사될 수 있으며, 대칭군 S_4를 갖는다.[1] 이는 (1, 2, 3, 4) 의 모든 순열이 3차원 부분 공간 x + y + z + w = 10 에서 깎은 정팔면체의 꼭짓점을 형성함을 의미한다.

3. 1. 아르키메데스 다면체

깎은 정팔면체는 13개의 아르키메데스 다면체 중 하나이다. 깎은 정팔면체의 쌍대 다면체는 사각육면체이다.[3] 둘 다 정팔면체와 동일한 3차원 대칭군인 정팔면체 대칭 \mathrm{O}_\mathrm{h} 를 갖는다.[4] 각 꼭짓점은 정사각형 하나와 육각형 두 개로 둘러싸여 있으며, 꼭짓점 도형은 4 \cdot 6^2 로 표시된다.[5]

깎은 정팔면체 단독에 의한 공간 채움


신라 시대 한국의 술래 도구. 전면을 사용하지만, 각 면을 거의 같은 면적으로 하기 위해 변형되어, 엄밀히 말하면 깎은 정팔면체는 아니다.


정팔면체


육방팔면체
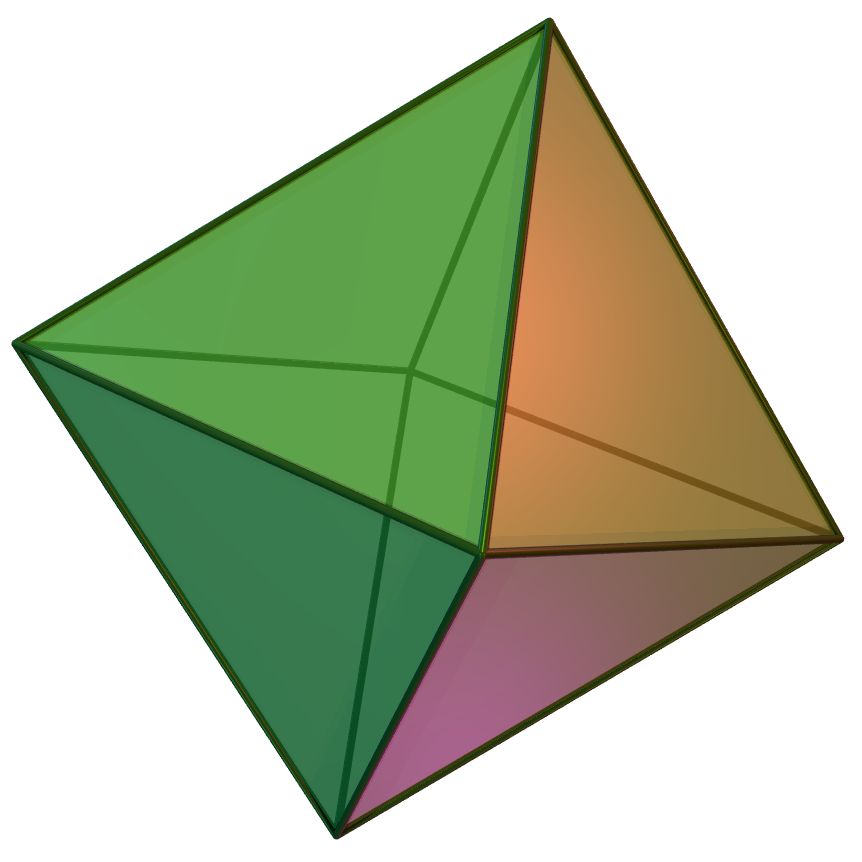
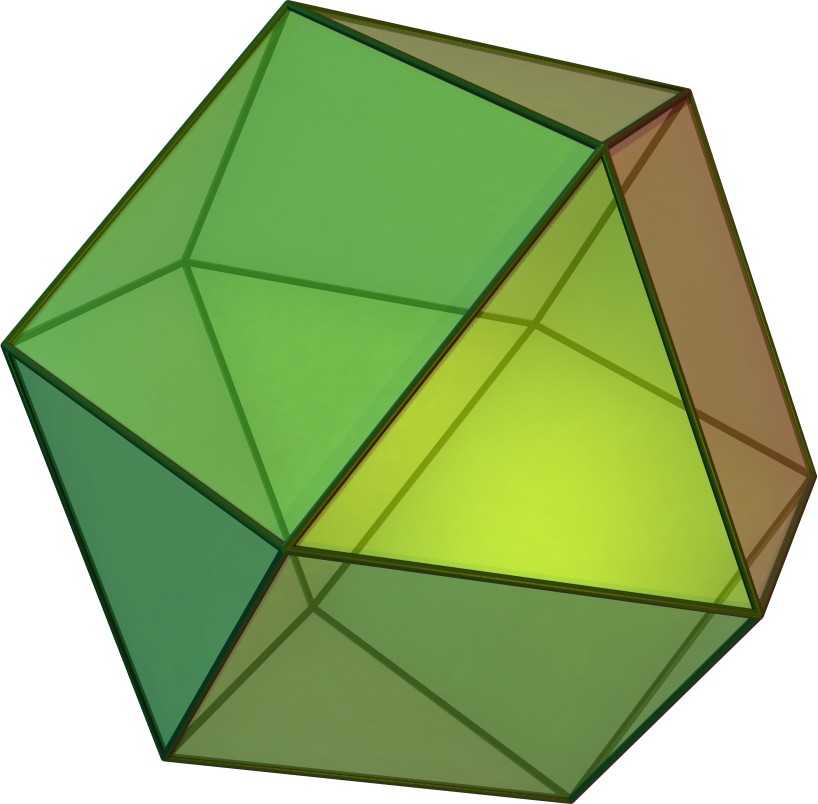
(깎기를 깊게 함)


깎은 정육면체
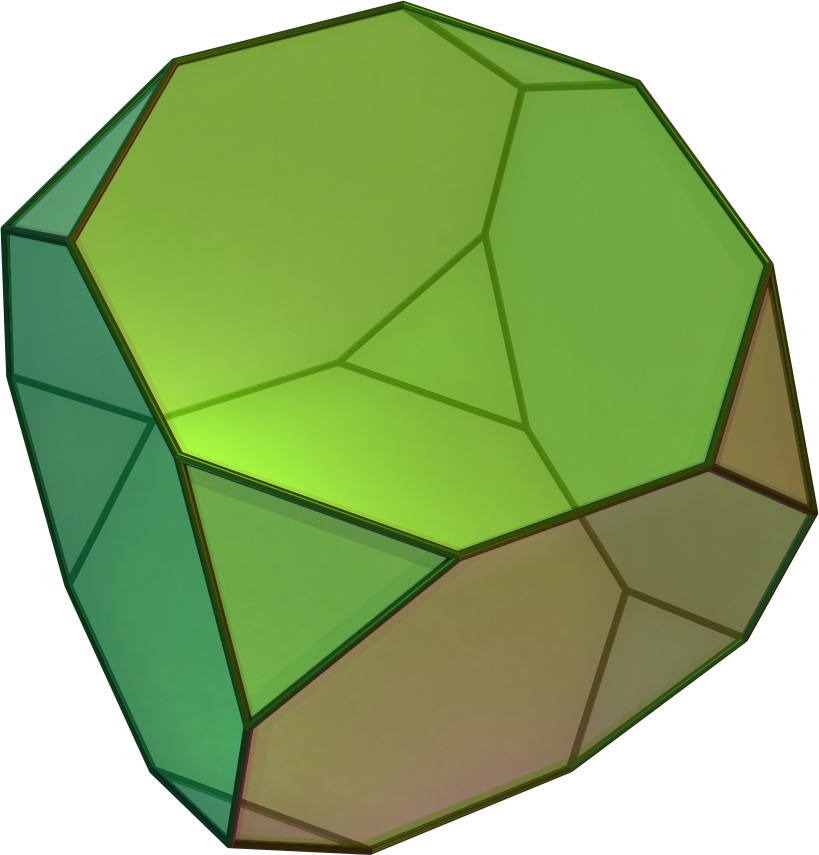
(깎기를 더욱 깊게 함)

3. 2. 공간 채움 다면체

깎은 정팔면체는 공간을 채울 수 있는 다면체이다. 이는 근접다면체로 분류되는데, 대칭적인 들로네 집합의 보로노이 셀로 정의될 수 있기 때문이다.[3] 회전 없이 평행이동된 근접다면체는 공간을 채우기 위해 반복될 수 있다. 깎은 정팔면체를 포함하여 5개의 3차원 기본 평행다면체가 존재한다.[4] 더 일반적으로, 모든 순열 다면체와 평행다면체는 존다면체인데, 이는 중심 대칭이며 민코프스키 합으로 정의될 수 있는 다면체이다.[5]

3. 3. 순열 다면체 (Permutohedron)

깎은 정팔면체는 4차 순열 다면체(4-permutohedron)로 묘사될 수 있으며, 대칭군 S_4를 갖는다.[1]

깎은 정팔면체는 4차 순열 다면체 또는 '''4차 순열 다면체'''로 묘사될 수 있다. 이는 4차원에서 더 대칭적인 좌표로 표현될 수 있음을 의미한다. 즉, (1, 2, 3, 4) 의 모든 순열은 3차원 부분 공간 x + y + z + w = 10 에서 깎은 정팔면체의 꼭짓점을 형성한다. 각 꼭짓점은 (1, 2, 3, 4) 의 순열에 해당하며, 각 모서리는 두 요소의 단일 쌍별 교환을 나타낸다.

깎은 정팔면체는 공간을 채울 수 있으며, 근접다면체로 분류된다. 이는 대칭적인 들로네 집합의 보로노이 셀로 정의될 수 있음을 의미한다. 회전 없이 평행이동된 근접다면체는 공간을 채우기 위해 반복될 수 있다. 깎은 정팔면체를 포함하여 5개의 3차원 기본 평행다면체가 있다.

4. 분해

깎은 정팔면체는 중앙의 정팔면체와 각 면에 8개의 삼각 컵(triangular cupola)과 꼭대기에 6개의 정사각뿔로 분해될 수 있다.[3]

중앙 정팔면체와 2개 또는 4개의 삼각 컵을 제거하면 이면각 대칭과 사면체 대칭을 가진 두 개의 스튜어트 토로이드(Stewart toroid)가 생성된다.

5. 응용

화학에서 깎은 정팔면체는 포자사이트형 제올라이트 결정의 골격에서 소달라이트 케이지 구조이다. 고체 물리학에서 면심 입방 격자의 제1 브릴루앙 영역은 깎은 정팔면체이다. 깎은 정팔면체는 반복 코딩과 함께 양자화 지수 변조(QIM)의 오류 분석에 나타난다.[2]

화학에서 깎은 정팔면체 구조를 갖는 제올라이트 (알루미노규산염)가 존재하는 것으로 알려져 있다. 소다라이트, A형 제올라이트, 포자사이트가 대표적이다.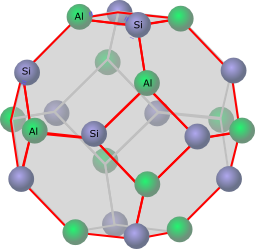

알루미노규산염에 의한 '''깎은 정팔면체''' 구조 (소다라이트 케이지)

6. 깎은 정팔면체 그래프

수학의 그래프 이론 분야에서 '''깎은 정팔면체 그래프'''는 깎은 정팔면체의 꼭짓점과 모서리의 그래프이다. 24개의 꼭짓점과 36개의 모서리를 가지며, 정육면체 아르키메데스 그래프이다.[5] 책 두께는 3이고 대기열 번호는 2이다.[6]

해밀턴 정육면체 그래프로서, LCF 표기법으로 여러 가지 방법으로 표현될 수 있다: [3, −7, 7, −3]6, [5, −11, 11, 7, 5, −5, −7, −11, 11, −5, −7, 7]2, 그리고 [−11, 5, −3, −7, −9, 3, −5, 5, −3, 9, 7, 3, −5, 11, −3, 7, 5, −7, −9, 9, 7, −5, −7, 3].[7]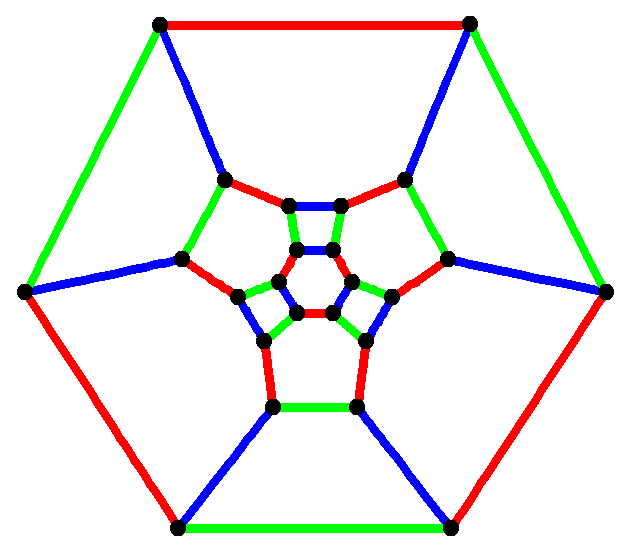

3배 대칭 슐레겔 도형


깎은 정팔면체 그래프에 대한 세 가지 다른 LCF 표기법에 의해 설명된 세 개의 다른 해밀턴 순환

7. 비슷한 다면체

정육면체


깎은 정육면체

육팔면체

깎은 정팔면체

정팔면체



8. 역사 속 깎은 정팔면체



신라 시대에는 깎은 정팔면체와 유사한 형태의 주사위가 술자리 게임(주령구)에 사용되었다. 각 면은 거의 같은 면적으로 변형되었기 때문에 엄밀히 말하면 깎은 정팔면체는 아니지만, 깎은 정팔면체의 형태와 기능을 이해하는 데 도움을 준다.

참조

[1] 웹사이트 Truncated Octahedron http://mathworld.wol[...]
[2] 논문 Performance analysis of existing and new methods for data hiding with known-host information in additive channels
[3] 웹사이트 Adventures Among the Toroids – Chapter 5 – Simplest (R)(A)(Q)(T) Toroids of genus p=1 http://www.doskey.co[...]
[4] 간행물 Mirrors and Reflections Springer
[5] 간행물 An Atlas of Graphs Oxford University Press
[6] 문서 Engineering Linear Layouts with SAT. University of Tübingen
[7] 웹사이트 Truncated octahedral graph
[8] 서적 Convex Polyhedra Springer
[9] 논문 Regular-faced convex polyhedra
[10] 논문 The Symmetry Group of the Permutahedron
[11] 서적 Multi-shell Polyhedral Clusters https://books.google[...] Springer Science+Business Media|Springer
[12] 논문 Zonotopes, dicings, and Voronoi's conjecture on parallelohedra
[13] 서적 Looking at Numbers https://books.google[...] Springer
[14] 논문 Convex polyhedra with regular faces
[15] 서적 Image Analysis: 21st Scandinavian Conference, SCIA 2019, Norrköping, Sweden, June 11–13, 2019, Proceedings Springer
[16] 서적 Mathematical Physics: Proceedings of the 13th Regional Conference, Antalya, Turkey, 27–31 October 2010 World Scientific
[17] 서적 Introduction to the Electron Theory of Metals https://books.google[...] Cambridge University Press
[18] 서적 The Geometrical Foundation of Natural Structure: A Source Book of Design https://archive.org/[...] Dover Publications, Inc.
[19] 서적 Chemical Processes for Environmental Engineering https://books.google[...] Imperial College Press


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com